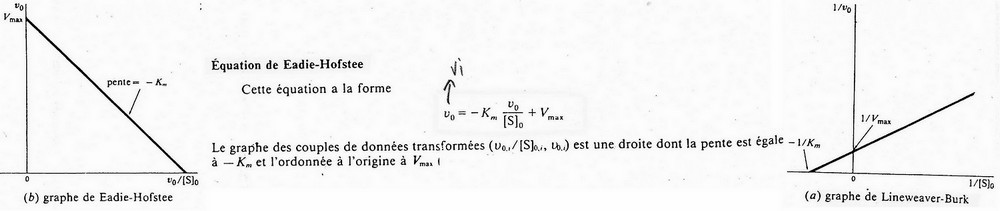Biochimie
Cinétique Enzymatique Michaélienne
1. La réaction enzymatique
Cinétique Enzymatique Michaélienne
1. La réaction enzymatique
v = d[P] / dt = d[S] / dt


Influence de la concentration en Enzyme

vi = f([E] . [S])
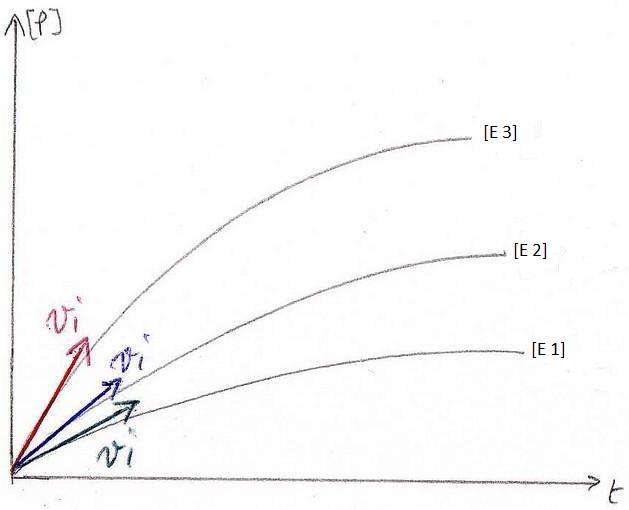


=> [S] élevée = vi = k . [E]
Remarque sur la courbe:
1: [E] = 0 --> vi ~ 0 --> la vitesse est négligeable
2: la zone linéaire stagne au bout d'un certain temps ( - - - - ). Si on augmente le concentration en substrat, alors la zone linéaire reprend.
Parfois, à partir d'une certaine concentration, la concentration en enzyme diminue, ce qui ne donne plus de zone linéaire.
Si on a: vi = k . [E] => [E] = 1/k . vi
On exprime [E] en « concentration catalytique ».
Influence de la concentration en Substrat
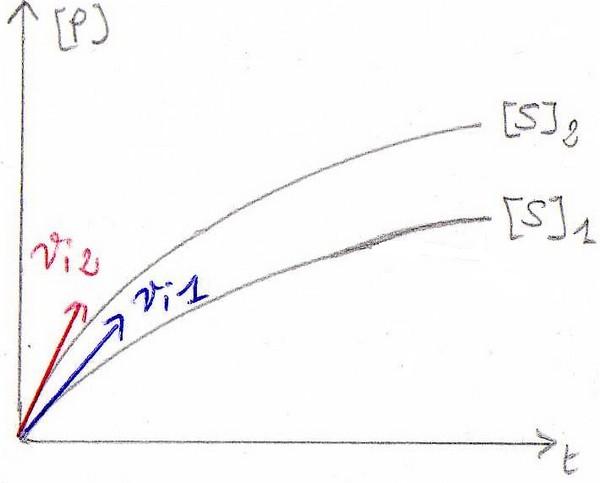

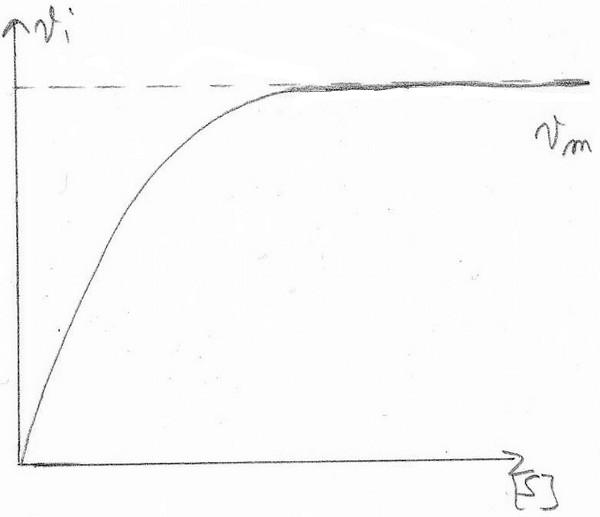
Vm = vi ([S] = ∞)
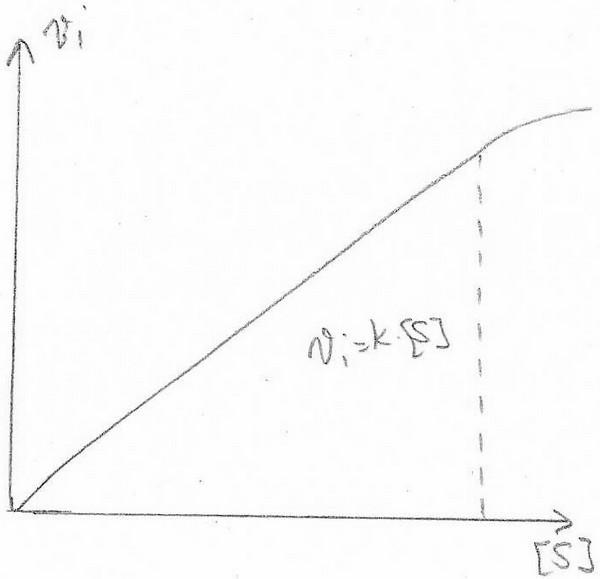
vi = k . [S]^n
L'ordre de la réaction varie en fonction de la concentration en Substrat
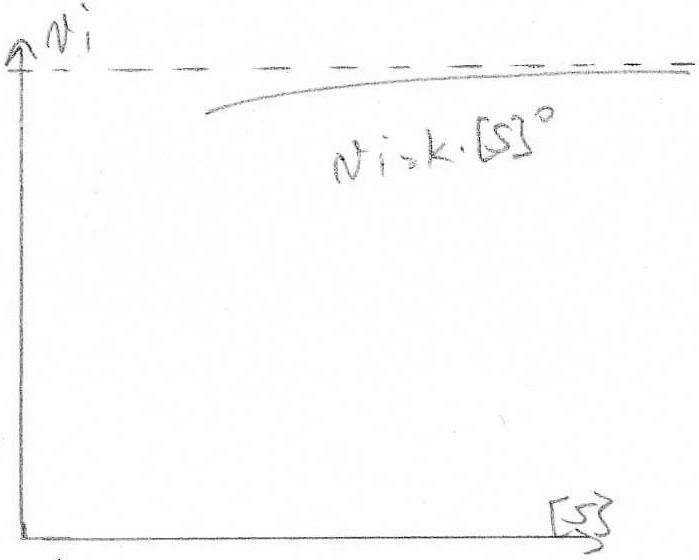
Hypothèse de Michaelis
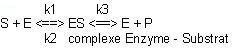
Hypothèse de Michaelis implique la Phase stationnaire
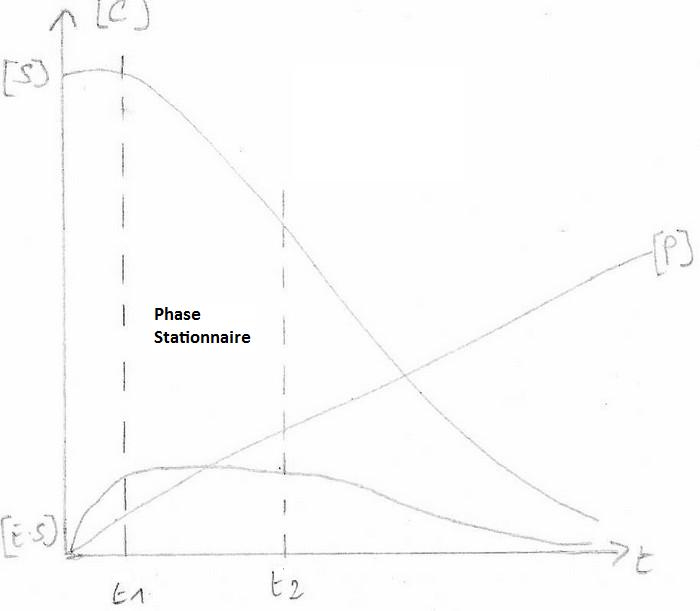
vi = d[P] / dt = d[S] / dt
vi = k3 . [ES]
La relation de Michaelis s'applique que pendant la phase stationnaire.
0 --> t1: phase préstationnaire, environ quelques secondes
=> inaccessible par des mesures classiques
t2 --> +∞: phase post-stationnaire
vi = d[P] / dt =constante = phase stationnaire
Si la phase stationnaire n'est pas visible, vi = tangente à la courbe
2. L'équation de Michaelis
Elle ne s'applique qu'en phase stationnaire
vi = constante
il faut que [P] soit négligeable donc E + P -X-> ES
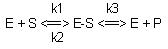
La constante de Michaelis
v1 = k1 . [E] . [S]
v2 = k2 . [ES]
v3 = k3 . [ES]
or -d[S] / dt = -k2 . [ES] + k1 . [E] . [S]
vitesse de disparition du substrat:
vi = d[S] / dt = k1 . [E] . [S] – k2 . [ES]
vitesse d'apparition du produit:
d[P] / dt = k3 . [ES]
Or – d[S] / dt = d[P] / dt
D'où:
k1 . [E] . [S] – k2 . [ES]=k3 . [ES]
k1 . [E] . [S] = k3 . [ES] + k2 . [ES] = (k3 + k2) . [ES]
=> (k3 + k2)/k1=([E] . [S])/[ES]
or k1, k2, k3 sont des constantes de vitesse d'où:
(k3 + k2)/k1=KM
Analogie avec l'équilibre chimique:
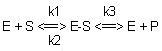
Donc KM est considéré comme une constante de dissociation « apparente » du complexe E-S.
K3 = s-1
nombre de molécules de Substrat transformées (ou de Produit formés) par un molécule d'Enzyme par seconde
Équation de Michaelis
[Et] = [E] + [ES]
KM = ([E] . [S]) / [ES] --> [E] = (KM . [ES]) / [S]
remplaçons:
[Et] = ( (KM . [ES]) / [S] ) + [ES]
multiplions par [S]
=> [Et] . [S] = (KM . [ES]) + [ES] . [S]
=> [Et] . [S] = [ES] . (KM + [S])
=> [ES] = ( [Et] . [S] ) / (KM + [S])
multiplions par k3
=> k3 . [ES] = k3 . ( ( [Et] . [S] ) / (KM + [S]) )
or vi = k3 .[ES]
=> k3 . [Et] = vi max
ce qui nous donne:
Vérification de la courbe expérimentale:
S très grand (par rapport ) KM) S>>KM
vi = (vi max . [S]) / (KM + [S]) alors vi = vi max
S très petit S<< KM
vi = (vi max . [S]) / (KM + [S]) = (v max . [S]) / KM
or v max /KM
Ainsi la relation de Michaelis est conforme au modèle
Vi = vi max / 2
vi = (v max . [S] ) / (KM + [S])
cas particulier:
v max / 2 = v max . [S] / KM + [S]
=> KM + [S] = 2[S]
donc KM = [S]
KM est la concentration en substrat quand vi = v max /2
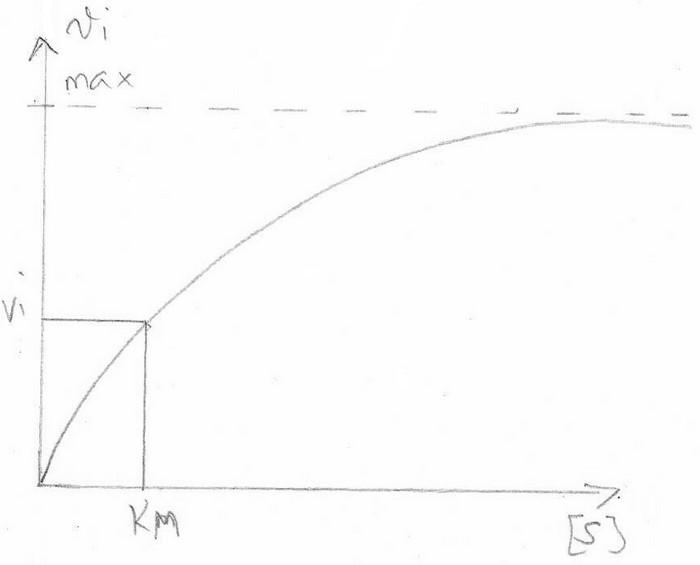
KM => constante d'association partielle
KM => (k2 + k3) / k1 = ([E] . [S]) / [ES]
Détermination de KM et Vm
Lineweaver et Burk (double inverse)
vi = (v max . [S]) / (KM + [S]) 1/ v i = (KM + [S]) / (V max . [S])
1/vi = ( (KM / v max) . (1/[S]) ) + ( ([S] / [S] ) . (1/v max) )
1/vi = (KM / v max) . (1/[S]) + (1/V max)
1/vi = f (1/[S])
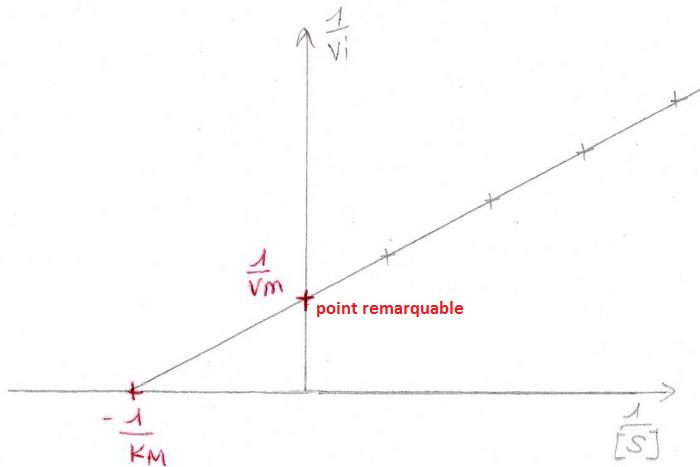
remplaçons:
1/vi = 1/v max
d'autre part:
1/vi = 0
0 = (KM / v max) . (1/ [S]) + (1/V max)
0 = KM / [S] + 1
=> KM / [S] = -1
d'où: 1/[S] = -1/KM
Cette méthode a un défaut: très souvent il faut négliger un point, celui qui a la plus petite [S]. Donc la droite retenue est nécessairement celle où on néglige ce point extrême.
Eadie
Vi = (V max . [S]) / (KM + [S])
(vi . (KM + [S]) ) / [S] = V max
vi = (KM / [S]) + Vi = Vmax => Vi = (-Vi / [S]) . KM + Vmax
y = -x . a + b
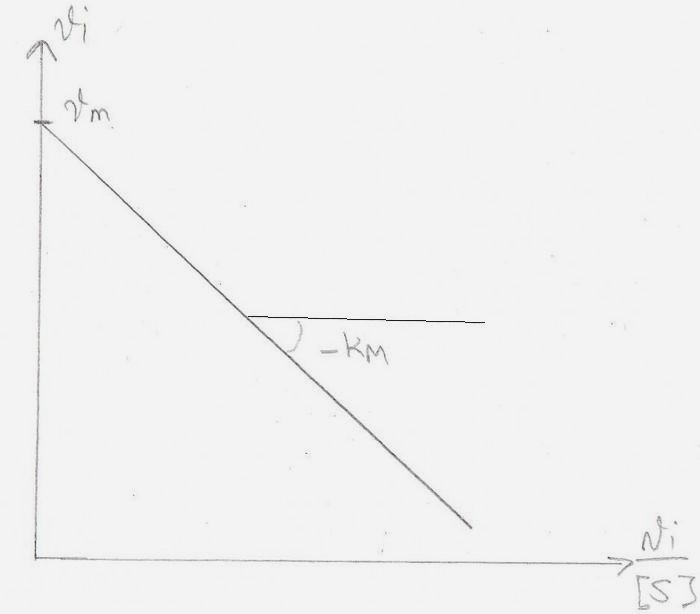
Eisenthal et Cornish-Bowden
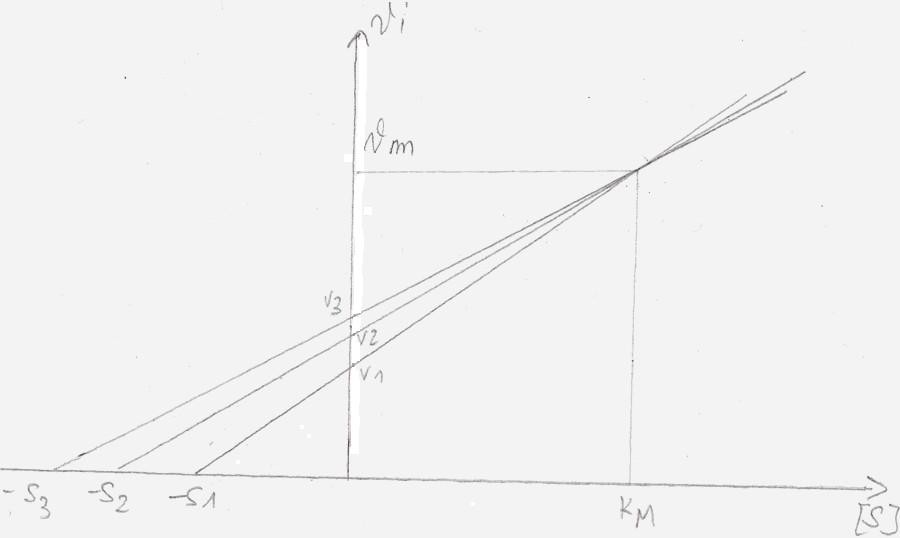
3. Calculs et significations des “constantes” en enzymologie
K M
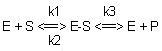
En général k3<
Si on ne tiens pas compte de la seconde réaction; on sait que:
Kass = k1 / k2 et Kdiss = k2 /k1 donc
KM = constante de dissociation apparente de complexe [ES]
=> reflet d'affinité de l'enzyme pour le substrat
Plus le KM est faible, plus l'enzyme a de l'affinité pour le substrat.
KM est une concentration, c'est [S] pour v i = v max / 2
On se rappelle:
vi = (v max . [S]) / (KM + [S])
si S>>KM : on néglige KM
--> Vi = (v max . [S]) / (KM + [S]) => Vi = V max
KM = 1mmol/L --> [S] = 10KM
Vi = (V max . 10KM) / (KM + 10KM)
vi = V max . 10/11 = 0,91 Vmax
KM = 1mmol/L --> [S] = 20KM --> Vi = Vmax . 20/21 = 0,95 Vmax
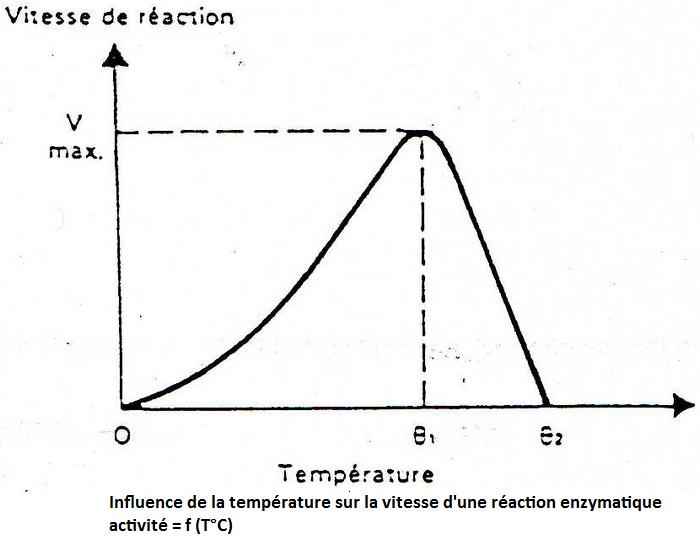
Attention: 1°C d'écart sur la température d ela réaction = 10% d'erreur sur la mesure
--> [S]>>20KM => Vi = 0,95Vmax
Vi ~ Vmax
Quand [S] couteux ou peu soluble on accepte:
[S]> 10KM => Vi = 0,91Vmax Vi =Vmax
« La concentration du substrat est dite saturante si [S]>20KM » --> alors l'enzyme est saturée.
Si S<
--> Vi = (Vmax / KM) . [S] or Vmax / KM = constante
d'où: vi = k . [S]
On dit que [S] < KM / 20
V max
Vi de la réaction quand [S] = + ∞;
quand [S]>20KM
Vmax = k3 . [E]t"(

-> soit KM est connu
[S]>>20KM Vi = Vmax une seule mesure
-> soit KM est inconnu
alors plusieurs mesures à des concentration de substrats variables
k3 = constante de Michaelis
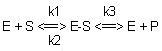
avec k3 t-1
Vmax en μmol/L/unité de temps
[E]t en μmol/L
Cela représente le nombre de mole de Substrat transformés ou de produit apparu par mole d'Enzyme et par unité de temps.
Les concentrations catalytiques
L'unité d'enzyme:
Quantité d'enzyme qui catalyse la transformation d'une μmole de substrat par minute, dans des
conditions définies (T°C, pH, présence éventuelle d'activateur, nature du substrat).
Le katal: peu utilisé
Quantité d'enzyme qui catalyse 1mole de substrat par seconde, dans des conditions définies.
4. Les limites du models Michaeliens
Tout ne se déroule pas comme Michaelis
Il faut être en Vitesse initiale Vi
Que S <--> P or ceci est rare, souvent S1 + S2 <--> P1 + P2
Enzyme monomérique
Inhibition par excès de Substrat
Le modèle de Michaelis n'est donc pas universel, il existe des limites.
5. Annexes.
Version imprimable en pdfShémas supplémentaires